
作者:新航道武汉学校-王海洋
部分,过往版本对比
试卷的单题阅读量加大
整张试卷的题量相较于前两年P1的考试:单题阅读量有所提升,一共九题,占据大概半页篇幅的题目有三题,接近一整页的题目有两题;单题分值增加,对步骤的要求更详细;总题量减少,整张卷子只有九题,跟之前几次考试的十题和十一题比起来是减少的,所以爱德思官方在单题阅读量增加的情况下,通过减少题量平衡了整张卷子的难度。这种调整说明了:①这种读题障碍的提升一方面会使得读题速度减慢,另一方面还会让解题思路的形成过程受阻。②语言作为基础数学中一直不受重视的部分,影响略微加大。
试卷的难度也有轻微的提升。
跟其他课程相反,这次爱德思基础数学的P1部分并没有因为疫情而让题目变得简单,整体难度是有一定提升的。这种难度的加大体现在三方面,①是单题阅读量的加大,已经提过了。②是最明显的一点,会将后续课程中的部分知识点隐藏在P1的考试中。比如第四题是圆的方程和直线方程联立,而圆的方程是P2部分第二章的内容;③是知识点覆盖很全面,仅仅只是9道题,但是覆盖了几乎所有的主流知识点。所以一本书中如果有任何一部分没有掌握好都会导致丢分。
第二部分,重点题目分析
第3题
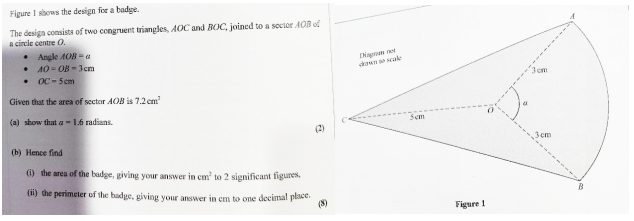
包含考点:
扇形面积公式,弧度制和角度制的转化,三角形面积公式,余弦定理,弧长公式。
解题思路:
a问:题目已知条件较多,已知扇形半径面积,可以利用扇形面积公式求扇形圆心角的弧度。
b问(i):总面积为两个全等三角形和扇形面积之和,因此最后的总面积是两个三角形面积的和再加上扇形面积,扇形面积已知。其实解题核心是算三角形面积,直接使用三角形面积公式的话还需要其夹角,夹角为2π减扇形圆心角的结果的一半即可。
b问(ii):求周长首先使用余弦定理求出三角形的钝角对边,再用弧长公式求出弧长,最后加总即可。
重难点解析:
其实整道题目解题的思路是比较好构建的,但是知识点的连接很紧密,考察全面,只要基本功扎实,这一题出现问题的概率都不大。此外,这一题跟书上第七章134页exercise7B第14题几乎一样,只是本次真题还加入了面积相关内容。所以说课本上的题目是一定要认真完成的,真题复现比例不低。
第5题
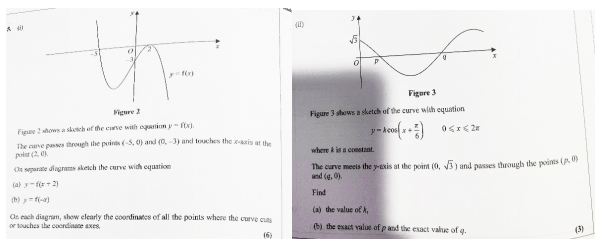
包含考点:
不给函数图形下的图形变换,主要是关于x的变换,三角函数图形的变换。
解题思路:
(i):第1部分主要考察了当X变动的情况下,整个函数图形的变换。从图形中我们可以看出,尽管它没有给我们直线方程,但这个图形其实是三次函数图形,然后给到了所有和XY轴的交点。那么我们在图形变换的时候,除了要满足我们在X变换时“加左减右乘薄除厚”“负x绕y轴对称”的规律,还要注意我们要把变换以后的点也都给标出来。
(ii):第2部分则是一个标准的三角函数图形的变化,第1题考察了代入。其实就是直接把题目给的坐标点带入到方程里面去,会得到一个关于x的三角的方程,解出这个方程就可以得到k的值,就相当于得出了这个新的三角函数的方程,再去判断它在0~2π之间和X轴的交点即可。
重难点解析:
这个题目第1部分的图形变换是非常规矩的,符合日常刷题的形式。而第2部分很多同学可能上手就想到去做图形变换,但其实它仅仅通过代数的计算就可以得到最后的结果。所以说第2部分会一定程度拖慢做题的速度。因此,对于第2部分这种题目而言,我们可以先观察一下它的代数方法好不好计算,再去看具体的图形变换。
第8题:

包含考点:
求导,求切线方程,平行的斜率变化以及切线和导函数的理解。
解题思路:
a 问:是一个非常典型的求导题目,所以这一题非常的简单。因为他已经把最后求导的结果告诉我们了,所以我们求导之后,可以根据他给我们的结果来判断我们是否算对了。而这个计算的过程无非就是多项式相乘的展开,以及整数幂的指数求导。
b问:则是求切线的方程,这个求切线的方程的题目非常的规律,和我们书本上做的题是一模一样的。严格按照书上例题步骤即可。
c问:则通过直线平行的这个性质告诉我们了新的直线的斜率,然后我们就相当于知道了这个新的直线方程,但是最后那个常数项c我们还未知。我们就可以斜率20带入到导函数中,会求出两个值,其中一个是上一问的6,另一个就是这一题的解了。
重难点解析:
这一题的前两问非常规律,非常规范,也非常的好做。但是第3问的这个做法就比较难了,其思路的构建要求我们对于函数的导数以及切线这几个相关概念具有非常高的熟练度。所以对于这一题而言,我们要多去了解一下它背后的出题逻辑,会对考试很有帮助。
第三部分,未来趋势预测
根据这一套卷子所表现出来的规律而言,未来一到两次的P1覆盖的知识点将会更加的全面;同时难度和题量趋于稳定。
备考建议:
① 每次考试之前都要进行一次全面的查漏补缺;
② 对待每一题我们需要把步骤写得更详尽;
③ 掌握了出题规律,会让看似越来越难的基础数学考试其实本质并没有变化太多;
④ 原题复现概率高,认真对待书中标红E的练习题。