SAT数学考点及易错点分析
作者:冉肖潇
SAT数学一直在SAT考试的总分中占据重要的位置,根据2018年和2019年已经考过的考试来说,SAT数学的要求逐渐增加,大家在拿高分和满分的路上需要做更多的准备,首先我们看一下SAT数学的考试范围分布情况:
|
知识点 |
题目个数 |
所占百分比 |
|
线性方程和函数 |
21 |
36% |
|
二次函数 |
6 |
10% |
|
比值,比率,百分比计算和数据分析 |
5 |
8% |
|
几何 |
5 |
8% |
|
统计学 |
5 |
8% |
|
方程组 |
4 |
7% |
|
多项式 |
3 |
5% |
|
不等式 |
2 |
4% |
|
指数函数 |
2 |
4% |
|
三角函数 |
1 |
2% |
|
单位换算 |
1 |
2% |
|
解析几何之圆的标准方差 |
1 |
2% |
|
复数 |
1 |
2% |
|
概率 |
1 |
2% |
从上表可以看出,线性方程和函数依然占据了近1/3的考题,依然是SAT数学考试的重点。
不同的是,统计学初步知识,比值和百分比计算,数据分析和几何问题有所增加。特比是在统计部分中连续出现关于箱线图,四分位数的考题,这在之前是没有出现过的。
常考知识点概述
线性方程和函数高频考点
在线性方程和函数中,关于直线的部分是一个非常高频考点,包括斜率,直线的方程,平面坐标系中直线与方程的关系(平行,垂直),x-intercept和y-intercept在应用题中的意义等。
例如2016年5月北美真题中,section 3 的第8题,问331.4的意义,其实转换成数学语言就是问y-intercept的意思,做这类题目时,把握好当x=0时,y值的意义就是关键。
1
类似的题目在2018年3月北美section4第11题,section4第24题,2018年3月亚太section4第12题,17题,2018年5月北美section4第15题,2018年5月亚太section3第11题等。
同样在平面坐标系中直线与方程的关系中平行和垂直也是需要我们注意到的高频考点,解题的关键在于抓住两条直线平行时,斜率相同,截距不同,垂直时,斜率互为负倒数。例如2017年11月北美真题section 4的36题

类似的题目在2018年3月北美section3第4题,section4第24题,2018年5月北美section3第16题,section 4 第35题,2018年5月亚太section 4第19题等
以及如何在通过题目给出的信息找到相应的图像,例如下题可以根据图形知道(3,0)和(0,2)两点求出斜率,继而进行后续的计算。
3
类似的题目在2018年3月北美section3第1题,section4第30题,2018年3月亚太section 3第18题,section4第9题,26题,2018年5月北美section3第6题,section4第13题,第25题,2018年5月亚太section3第2题等。
通过未知数来表述问题,列出方程,解决实际问题也是我们这一类的高频考点。例如2018年3月亚太真题section3的2题,这类题目的重点在于先定义/找出一个或者多个表示数量的变量,再根据题意,每句话列出相应表达式,方程,不等式或者函数。

类似的题目在2018年3月北美section3第2题,2018年3月亚太section 3第2题,2018年5月北美section3第1题,section4第4题,第25题,2018年5月亚太section4第28题等。
值是这部分的另外一个考点,做值的题目时要把握做以下几点:“l l”大于等于0和检查多种答案的可能性。例如:2016年5月亚太真题section4的28题
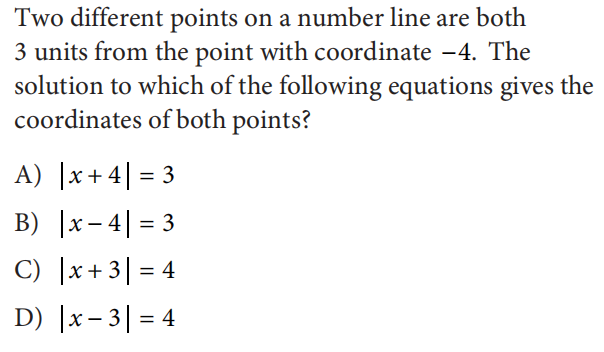
类似的题目在OG1 section3第8题,OG4 section3 第1题,2017年5月亚太section 3 第16,2018年3月亚太section 3第9题等。
二次函数高频考点在于解一元二次方程,函数的各种性质(开口方向,对称轴,顶点坐标,解的个数等)和表达式,韦达定理等。例如

这类题目只学要记住就可以避免大量运算。以及我们应了解因式分解,求根公式。
类似的题目在2017年12月亚太section3第18题,section 4第8,32题,2018年3月北美section3第3,7,10,section 4第1,,27题,2018年3月亚太section 3第11题,section4第10,30题,2018年5月北美section3第5,8题,section4第18题,2018年5月亚太section3,第13,15题,section4第5,25,30题等。
比值,比率,百分比计算和数据分析这类题目喜欢出现在图表题里,图表题的关键就是要读懂表格和XY横纵坐标的意义,善于转换数学单位以及理解并分析不同变量之间的关系。百分比的计算要抓住的重点在于题目中的增加/减少百分比如何计算,例如OG2section4中第20题,虽然比重一样,但是图表下方的信息显示总数不同。


类似的题目在2017年12月亚太section4第16,17,2637,38题,2018年3月北美section 4第20,37,38题,2018年3月亚太section 4第8,22,37,38题,2018年5月北美section4第20-22题,2018年5月亚太section4第18,38题等。
几何高频考点主要是在于三角形相似,平行的运用和圆形及其他几何图形性质理解,面积体积公式,考试会有提供,主要的重点在于灵活运用这些性质。例如:OG1 section3第17题,利用相似解决问题。
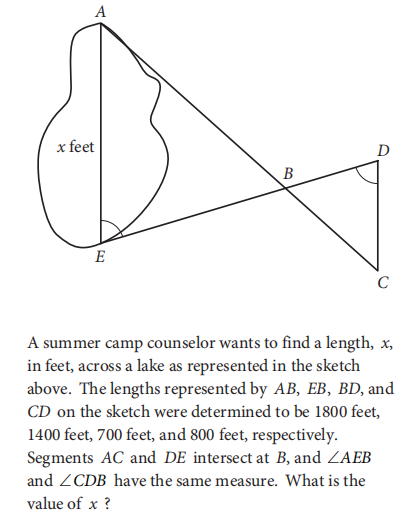
类似的题目在2017年12月亚太section3第12题,2018年3月北美section 4第16题,2018年3月亚太section 3第10题,2018年5月北美section4第12题,section4第4题,第36题,2018年5月亚太section3,第7题,section4第16,33,37题等。
统计学高频考点主要是掌握统计知识的一些基本概念,例如总体population size,包含研究的全部个体(数据)的集合;样本sample,从总体中抽出的一部分元素的集合;样本容量或样本量sample size构成样本的元素数目;误差margin of error。统计题目中把握一下原则,样本抽样随机和样本数量足够大以及牢记样本特征。例如:
统计学中最近出现了以前不太常考的新的概念,箱线图和四分位数。箱线图(Boxplot)也称箱须图(Box-whisker Plot),是利用数据中的五个统计量:最小值、四分位数、中位数、第三四分位数与值来描述数据的一种方法,它也可以粗略地看出数据是否具有有对称性,分布的分散程度等信息,特别可以用于对几个样本的比较。

如图L表示最小值,G表示值,Q1为个4分位数,M为中位数,Q3为第三个四分位数,G为值。例如我们在2019年3月北美section 4的32题
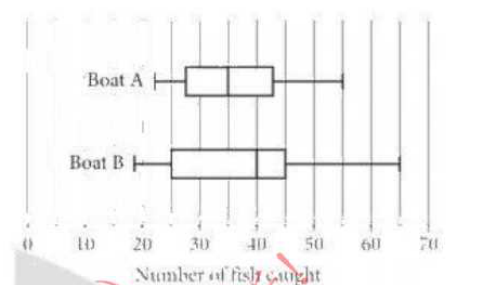
The box plots above summarize the distribution of the number of fish caught each day on two commercial fishing boats for a season. By how many fish does the median number of fish caught each day on Boat B exceed the median number on Boat A?
如图可知Boat A的中位数为35,Boat B的中位数为40,答案应为40-35=5
类似的题目在2019年3月亚太section4 第3题和2018年3月北美section4第29题。
四分位数(Quartile)应用于统计学中的箱线图绘制,是统计学中分位数的一种,即把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。四分位数 (Q1),又称“较小四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。第二四分位数 (Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。第三四分位数 (Q3),又称“较大四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。
指数函数高频考点首先需要我们牢记指数运算法则并会灵活运用,第二能够在应用题中代入指数函数解题。指数运算法则为
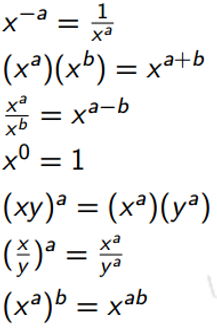
13例如2018年3月北美section3第15题

类似的题目在2016年5月北美section3第12题,2017年12月亚太 section3第1题,2018年3月北美section4 第21题,等。
三角函数高频考点把握住sin cos tan的意义以及需要了解当sin x=cos y则有x+y=90这个性质即可,例如OG1 section3第19题sin x=cos(90°- x)=4/5
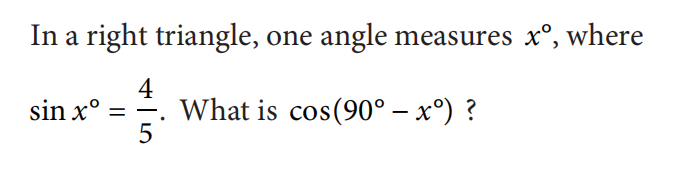
类似的题目在2018年3月北美 section3第16题,section4 第23题,2018年5月北美section 3 第19题等。
解析几何之圆的标准方差一定要记住圆的标准方程是(x-a)²+(y-b)²=r²中,有三个参数a、b、r,即圆心坐标为(a,b)和半径r,以及弧度制和度之间的转换关系,例如在2016年5月北美section4 中第29题,首先需要把式子通过配方变成我们熟悉的圆的标准方程是(x+10)²+(y+8)²=144,从而得到圆的圆心坐标为(-10,-8)。

类似的题目在2018年3月北美 section4第36题,2018年3月亚太section4 第23题,2018年5月北美section 3 第15题等。
弧度制与度之间的转换也是另一个高频考点,例如OG2section3中第19题中可以算出∠AOB=30°根据弧度与角度的转换关系知道应π/6,即a=6。
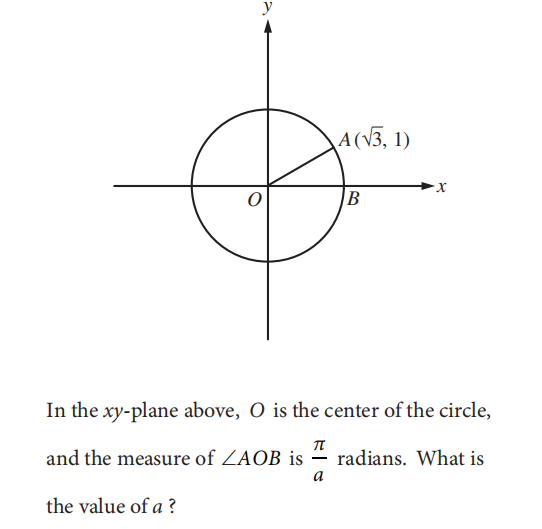
类似的题目在OG3 section4第34题,OG4 section4第24题,2016年5月亚太section3 第20题,2018年3月北美section3第19题,2018年5月亚太section 3 第20题等。
复数这部分的考点不熟悉主要是因为对复数知识的不了解。复数的定义为形如z=a+bi(a,b均为实数)的数称为复数,其中a称为实部,b称为虚部,i称为虚数单位。
当虚部等于零时,这个复数可以视为实数;当z的虚部不等于零时,实部等于零时,常称z为纯虚数。复数的运算法则为主要考点,例如OG1 section3第2题,做题是把握住复数的运算法则即可。

类似的题目在2017年12月亚太 section3第20题,2018年3月亚太section3 第6题,2018年5月北美section 3 第20,2018年5月亚太section 3第18题等。
易错丢分点
以上为SAT数学中的高频考点,根据统计表明在SAT数学中考高分容易,考满分难。问题一般在于以下几点:
,粗心马虎,例如读题不仔细,题目需要求5X,但是得到X直接作答。
第二,不熟悉数学的英文表达,身陷语言陷阱中,例如Percent More,What number is 250% more than 50? 这个文字问题的表述,比50多250%,很多人都会直接用50去乘以2.5,而这种理解本身就有错误。正确解读应该是比50多250%,那么就应该在50的基础上再加上多出的部分,也就是2..5*50 + 50,也就是(2.5+1)(50),这个文字问题在SAT数学的实际应用类问题中尤为常见,各位同学一定要多加小心。例如
|
Factors and Divisors: A×B=C |
A and B are factors of C |
|
A and B are divisors of C |
|
|
C is divisible by A and by B |
|
|
C is a multiple of A and of B |
|
|
A=nB |
A n times as many as B |
|
n times A as many as B |
|
|
n times as many A as B |
|
|
A - B |
from A subtract B |
|
B less than A |
|
|
A less B |
|
|
用 x 表示 y |
y in terms of x |
第三,知识点不熟悉或者公式记忆混乱。例如完全平方公式和平方差公式混乱。例如OG2 section3第4题和2016年5月亚太section3第4题。

以下为我们需要记忆的基本公式
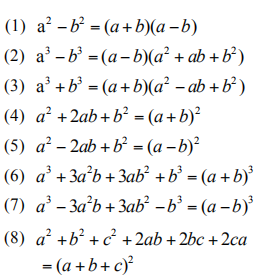
第四,练习过少,速度不够,时间紧张。需要同学们课下多多练习,总结错题来提高速度跟正确率。
第五,固定思维,无法灵活变通。例如OG4 Section3第9题,可以直接带入选项验证更快,和OG4 Section3第18题,应两两配对,而不是把常数项转移到右边。当平时练习遇到此类题型时,应做上记号,方便后期复习与整理。
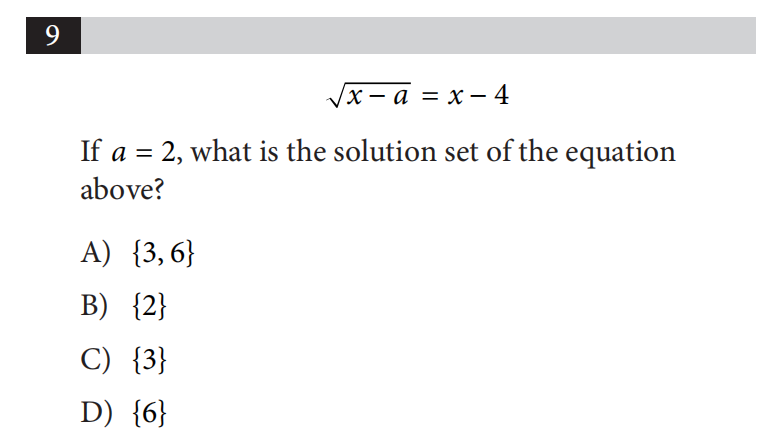
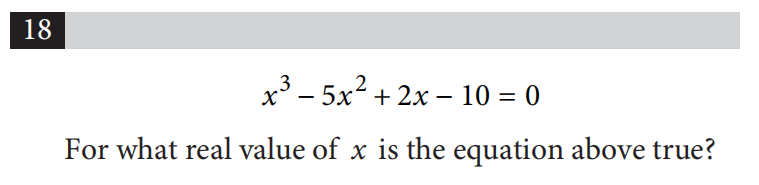
推荐阅读
- SAT文法考试标点题中的逗号考点
- SAT数学考点及易错点分析
- AP Calculus备考建议
- AP 物理考试一站式指南
- SAT数学考试知识点范围归纳
- 2018官方新SAT/ACT分数对照表
- SAT写作高分攻略
【本文标签】:
【责任编辑】:武汉新航道小编 版权所有:转载请注明出处


